{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение.
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит
название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. {2}}}}$$
{2}}}}$$
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
| 3. Решение задач | |
| 1. Как будем выставлять оценку за работу на
уроке по принципу сложения или вычитания? |
По принципу сложения. |
| 2. Таблица 1 (Приложение №1). На
складе имеются грузы: мел, пробка, береза, лед, сталь. Каждый груз упакован в контейнеры по 2 м3. для перевозки этих грузов были вызваны пять автомобилей. Ваша задача распределить грузы по автомобилям. |
Найти массу грузов. |
| — Что нужно сделать, чтобы распределить грузы
по автомобилям? |
|
| — Как найти массу вещества, если известна его
плотность и объём? |
кг/м3 |
| — В каких единицах измерена плотность вещества? | В килограммах |
| — В каких единицах будет вычислена масса? | В тоннах и килограммах |
| — В каких единицах выражена грузоподъемность
автомобилей? |
В тоннах, а для москвича в килограммах |
| — В каких единицах нужно получить массу грузов?
Решите
Учитель проверяет правильность выполненного
|
Ученики решают задачи и распределяют грузы. |
| 3. Таблица 2 (Приложение № 2).
Имеются пять различных жидкостей, которые имеют одинаковую массу. Эти жидкости нужно разлить по пяти различным сосудам. — Что нужно сделать,
|
Найти объём жидкостей. |
| — Как найти объем, если известна масса вещества
и его плотность? |
|
| — В каких единицах получится вычисленный объём? | в м3. |
| — В каких единицах дан объём сосудов? | В литрах и миллилитрах |
| — В каких единицах нужно получить объём
жидкостей? |
В литрах и миллилитрах |
| Решите данную задачу и распределите жидкость
по сосудам. 
Учитель проверяет правильность
|
Ученики решают задачу. |
| 4. Рефлексия. | |
| — Какие физические понятия Вы использовали для
выполнения заданий? Сравните количество баллов,
Готовы ли вы к контрольной работе? |
Масса, плотность, объем. |
Плотность вещества — как определить и чему равна?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Масса
Начнем с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.
Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.
В Международном бюро мер и весов в Париже есть цилиндр массой один килограмм. Материал этого цилиндра — сплав иридия и платины. Его масса равна одному килограмму, и этот цилиндр — эталон для всего мира.
Высота этого цилиндра приблизительно равна 4 см, но чтобы его поднять, нужно приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.
|
Второй закон Ньютона F = ma F — сила [Н] m — масса [кг] a — ускорение [м/с2] |
В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.
Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.
|
Закон Всемирного тяготения F = GMm/R2 F — сила [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6.67 × 10-11 м3 кг-1 с-2 |
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне🙃
Откуда берется масса
Физики убеждены, что у элементарных частиц должна быть масса. Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.
Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.
Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не существовало бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.
Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.
Источник: Википедия
Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.
Объем тела
Объем — это физическая величина, которая показывает, сколько пространства занимает тело. 3]
3]
Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.
Маленькое исключение
Исключение составляет вода. Так, плотность воды меньше плотности льда. Объяснение кроется в молекулярной структуре льда. Когда вода переходит из жидкого состояния в твердое, она изменяет молекулярную структуру так, что расстояние между молекулами увеличивается. Соответственно, плотность льда меньше плотности воды.
Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.
|
Твердое вещество |
кг/м3 |
г/см3 |
|
Платина |
21500 |
21,5 |
|
Золото |
19300 |
19,3 |
|
Вольфрам |
19000 |
19,0 |
|
Свинец |
11400 |
11,4 |
|
Серебро |
10500 |
10,5 |
|
Медь |
8900 |
8,9 |
|
Никель |
8800 |
8,8 |
|
Латунь |
8500 |
8,5 |
|
Сталь, железо |
7900 |
7,9 |
|
Олово |
7300 |
7,3 |
|
Цинк |
7100 |
7,1 |
|
Чугун |
7000 |
7,0 |
|
Алмаз |
3500 |
3,5 |
|
Алюминий |
2700 |
2,7 |
|
Мрамор |
2700 |
2,7 |
|
Гранит |
2600 |
2,6 |
|
Стекло |
2600 |
2,6 |
|
Бетон |
2200 |
2,2 |
|
Графит |
2200 |
2,2 |
|
Лёд |
900 |
0,9 |
|
Парафин |
900 |
0,9 |
|
Дуб (сухой) |
700 |
0,7 |
|
Берёза (сухая) |
650 |
0,65 |
|
Пробка |
200 |
0,2 |
|
Платиноиридиевый сплав |
21500 |
21,5 |
|
Жидкость |
кг/м3 |
г/см3 |
|
Ртуть |
13600 |
13,6 |
|
Мёд |
1300 |
1,3 |
|
Глицерин |
1260 |
1,26 |
|
Молоко |
1036 |
1,036 |
|
Морская вода |
1030 |
1,03 |
|
Вода |
1000 |
1 |
|
Подсолнечное масло |
920 |
0,92 |
|
Нефть |
820 |
0,82 |
|
Спирт |
800 |
0,8 |
|
Бензин |
700 |
0,7 |
|
Газ |
кг/м3 |
|
Хлор |
3,22 |
|
Озон |
2,14 |
|
Пропан |
2,02 |
|
Диоксид углерода |
1,98 |
|
Кислород |
1,43 |
|
Воздух |
1,29 |
|
Азот |
1,25 |
|
Гелий |
0,18 |
|
Водород |
0,09 |
Где самая большая плотность?
Самая большая плотность во Вселенной — в черной дыре. Плотность черной дыры составляет около 1014 кг/м3
Плотность черной дыры составляет около 1014 кг/м3
Средняя плотность
В школьном курсе чаще всего говорят о средней плотности тела. Дело в том, что если мы рассмотрим какое-нибудь неоднородное тело, то в одной его части будет, например, большая плотность, а в другой — меньшая.
Если вы когда-то делали ремонт, то знакомы с такой вещью, как цемент. Он состоит из двух веществ: клинкера и гипса. Значит нам нужно отдельно найти плотность гипса, плотность клинкера по формуле, указанной выше, а потом найти среднее арифметическое двух плотностей. Можно сделать так.
А можно просто массу цемента разделить на объем цемента и мы получим ровно то же самое. Просто в данном случае мы берем не массу и объем вещества, а массу и объем тела.
|
Формула плотности тела р = m/V р — плотность тела [кг/м^3] m — масса тела [кг] V — объем тела [м^3] |
Решение задач: плотность вещества
А теперь давайте тренироваться!
Задача 1
Цилиндр 1 поочерёдно взвешивают с цилиндром 2 такого же объёма, а затем с цилиндром 3, объем которого меньше (как показано на рисунке).
Какой цилиндр имеет максимальную среднюю плотность?
Решение:
Плотность тел прямо пропорциональна массе и обратно пропорциональна объему:
р = m/V
Исходя из проведенных опытов можно сделать следующие выводы:
1) масса первого цилиндра больше массы второго цилиндра при одинаковом объеме. Значит плотность первого цилиндра выше плотности второго.
2) масса первого цилиндра равна массе третьего цилиндра, объем которого меньше. Следовательно, плотность третьего цилиндра больше плотности первого цилиндра.
Таким образом, средние плотности цилиндров:
р2 < р1 < р3
Ответ: 3.
Задача 2
Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (как показано на рисунке). Для объёмов шаров справедливо соотношение V1 = V3 < V2.
Какой шар имеет максимальную среднюю плотность?
Решение:
Из рисунка ясно, что масса шаров 1 и 2 равна — следовательно, плотность второго шара меньше, чем первого. 3
3
Плавание тел
Почему шарик с гелием взлетает? Или мяч при игре в водное поло не тонет?
Жидкости и газы действуют на погруженные тела с выталкивающей силой. Подробно это явление рассматривают в теме «Сила Архимеда». Если говорить простым языком: если плотность тела, погруженного в воду, больше плотности воды — тело пойдет ко дну. Если меньше – оно всплывет на поверхность.
Задача 1
Стальной шарик в воде падает медленнее, чем в воздухе. Чем это объясняется?
Решение:
Плотность воды значительно выше, чем воздуха, поэтому стальной шарик в воде падает медленнее
Задача 2
В таблице даны плотности некоторых твердых веществ. Если вырезать из этих веществ кубики, то какие кубики смогут плавать в воде? Плотность воды — 1000 кг/м3.
|
Название вещества |
Плотность вещества, кг/м3 |
|
Алюминий |
2700 |
|
Парафин |
900 |
|
Плексиглас |
1200 |
|
Фарфор |
2300 |
|
Сосна |
400 |
Решение:
Плавать будут кубики, плотность которых меньше плотности воды, то есть сделанные из парафина или сосны.
Масса покоя или инертная масса?
Масса покоя или инертная масса?
УДК. 12:531.18+51]
Масса покоя или инертная масса?
Р. И. Храпко
Исключение из современных учебников
физики инертной массы и замена ее массой покоя
представляется ошибкой. Эта тема была поднята
автором в статье [1,2].
Здесь приведены дополнительные рассуждения в
подтверждение такого тезиса.
Конец 20-го века ознаменовался великой
путаницей с физическим понятием «масса
тела».
1. Масса покоя
В начале века, до создания теории
относительности, было все ясно. Массой тела, m, называлось количество вещества
тела, и в то же время масса являлась мерой
инертности тела. Инертность тела определяет его
Инертность тела определяет его
«количество движения» при заданной скорости
v движения, то есть
коэффициент пропорциональности в формуле
P = mv. (1)
P — количество движения или,
по-научному, импульс тела, а коэффициент m называется инертной массой.
Но массу как меру инертности тела
можно определять и с помощью формулы
F = ma: (2)
чем больше масса, тем меньше ускорение тела при
заданной силе. Значение массы по формулам (1) и (2)
получалось одно и то же, потому что формула (2)
является следствием формулы (1), если инертная
масса не зависит от времени и скорости.
То же значение массы можно было
получить, взвесив тело, то есть измерив силу
притяжения к земле или к любому другому
заданному телу (масса которого обозначена M). В законе тяготения Ньютона
фигурирует та же самая масса m,
, (3)
но тут она называется гравитационной
(пассивной) массой. В этом выражается
эквивалентность инертной и гравитационной
массы. Благодаря этой эквивалентности ускорение
свободного падения, как известно, не зависит от
природы и массы тела:
(4)
2. Инертная масса
Однако при создании теории
относительности выяснилось, что никакое тело
нельзя разогнать до скорости света, потому что
при приближении скорости тела к скорости света
ускорение тела уменьшается до нуля, как бы ни
была велика ускоряющая сила. Другими словами,
выяснилось, что инертность тела возрастает до
бесконечности при приближении его скорости к
скорости света, хотя «количество вещества»
тела, очевидно, остается при этом неизменным.
Выскажемся точнее по поводу
увеличения инертности тела. Теория
относительности показала, что импульс тела P при любых скоростях остается
параллелен скорости v.
Поэтому формулу P = mv можно сохранить неизменной при
больших скоростях, если принять, что коэффициент m, то есть инертная масса,
увеличивается с ростом скорости по закону
, (5)
то есть для импульса тела справедливо
выражение
. (6)
(6)
В этих формулах m0 — это то значение массы
рассматриваемого тела, о котором говорилось
вначале, то есть значение, которое можно получить
после того, как тело затормозят до достаточно
малой скорости. Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
«до теории относительности» корректна.
Для того, чтобы подчеркнуть, что
инертная масса m зависит
от скорости, ее называют иногда
«релятивистской» массой: она оказывается
различной с точки зрения различных наблюдателей,
если эти наблюдатели движутся друг относительно
друга. Однако существует выделенное значение
инертной массы, именно, значение, которое
наблюдает неподвижный относительно тела
наблюдатель. Другими словами, масса покоя
Другими словами, масса покоя
является выделенным значением инертной массы.
Такое свойство инертной массы аналогично
свойству времени: одни и те же часы имеют разную
скорость хода с точки зрения различных
наблюдателей. Однако существует собственная
скорость хода часов.
При желании проверить формулу (6) вы
должны измерить скорость v тела, а потом измерить импульс тела.
Для этого следует затормозить тело некоторой
преградой, все время замеряя силу F(t), с которой при торможении тело
будет действовать на преграду, а потом
проинтегрировать. Импульс, как известно, равен
(7)
Эта процедура, по сути, задает операционное
определение инертной массы.
Заметим, что формулы (5) и (6) остаются
справедливыми и для объекта, у которого нет массы
покоя, m0 = 0,
например, для фотона или нейтрино (если
предположить, что масса покоя нейтрино равна
нулю). Такие объекты обладают инертной массой и
импульсом, но должны двигаться со скоростью
света, их нельзя остановить, они исчезают при
остановке. Тем не менее, несмотря на постоянство
Тем не менее, несмотря на постоянство
скорости движения, величина их
инертной массы оказывается различной с точки
зрения различных наблюдателей. Однако в этом
случае не существует какого либо выделенного
значения инертной массы. Либо, можно сказать,
выделенное значение равно нулю.
Увеличение инертности тела при
больших скоростях мы объяснили уменьшением
ускорения при большой скорости. При этом мы
сослались на формулу (2). И это допустимо. Однако
именно в силу увеличения инертной массы с ростом
скорости тела формула (2) при некоторых условиях
изменяет свой вид. Это объясняется тем, что при
фиксированном ускорении сила, если она имеет
составляющую вдоль скорости, должна обеспечить
не только возрастание скорости уже имеющейся
массы
, (5)
она должна обеспечить возрастание самой массы:
. (8)
Коэффициент
называют иногда продольной массой [3] .
Если сила перпендикулярна скорости и, значит,
не изменяет величину скорости и инертной массы,
то формула F = ma
сохраняет свой вид:
. (9)
(9)
Последнее обстоятельство позволило Р.
Фейнману предложить простой способ
операционного определения инертной массы,
основанный на формуле (9) и справедливый для любой
скорости. «Массу можно измерить так: просто
привязать предмет на веревочке, крутить его с
определенной скоростью и измерять ту силу,
которая необходима, чтобы удержать его.» [4]
При произвольном направлении силы
относительно скорости тела коэффициент
пропорциональности в формуле (2) следует
рассматривать как некий оператор (тензор),
превращающий вектор a
в вектор F: F = a. Оператор зависит от величины и
направления скорости тела и, вообще говоря,
изменяет направление вектора. Это нетрудно
принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело — это внешний по
отношению к телу фактор. Понятно, что результат
воздействия силы, то есть ускорение a тела, может зависеть от соотношения
направлений векторов F
и v.
3. Гравитационная масса
Одновременно теория относительности
показала, что не только инертность тела, но и его
вес увеличивается с ростом скорости, причем по
тому же закону (5) в соответствии с
эквивалентностью инертной и гравитационной
массы. Поэтому формула (8) для тела, падающего вниз
со скоростью v, выглядит,
грубо говоря, так:
= .
Точная формула для ускорения может
быть получена в рамках общей теории
относительности, как показано в конце статьи:
, . (10)
Эта формула является релятивистским аналогом
формулы (4).
4. Энергия
Теория относительности показала далее, что
прирост инертной массы, m — m0, умноженный на квадрат скорости
света, равен как раз кинетической энергии тела:
(m √ m0)c2 = Ek.
(11)
Поэтому, если приписать покоящемуся
телу энергию покоя E0 = m0c2, то полная энергия E = E0
+ Ek тела оказывается
пропорциональной инертной массе:
E = mc2 (12)
Эта знаменитая формула Эйнштейна
провозглашает эквивалентность инертной массы и
энергии. Два, доселе различных понятия,
Два, доселе различных понятия,
соединяются в одно.
Заметим, что формула (12), как и формулы
(5) и (6) остается справедлива и для объекта, у
которого нет массы и энергии покоя, m0
= 0.
При желании проверить формулу (11) и
одновременно убедиться в справедливости теории
относительности вы должны измерить инертную
массу и массу покоя тела как было объяснено выше,
и, кроме того, измерить кинетическую энергию
тела. Для этого следует при торможении тела
упомянутой преградой все время замерять силу, с
которой тело будет действовать на преграду в
процессе торможения в функции перемещения l
преграды, F(l), а потом проинтегрировать.
Кинетическая энергия, равная, как известно, в
данном случае работе, вычисляется по формуле
.
Здесь F(l)dl — скалярное произведение силы на
инфинитезимальный вектор смещения преграды. Все
это рассказано в [5] .
Формула (11) связывает инертную массу,
массу покоя и кинетическую энергию. Используя
формулу (6) для вычисления разности m2
√ P2/c2, легко
связать инертную массу, массу покоя и импульс:
. (13)
Для частиц с нулевой массой покоя получаем mc
= P или E = Pc.
5. Система тел
При объединении нескольких тел в систему тел,
как известно, их импульсы и их инертные массы
складываются. Для двух тел это выглядит так:
P = P1 + P2,
m = m1 + m2. (14)
Другими словами, импульс и инертная
масса аддитивны. Не так обстоит дело с массой
покоя. Из формул (13), (14) следует, что масса покоя
пары тел с массами покоя m01, m02 равна не сумме m01 + m02, а сложному выражению, зависящему от
импульсов P1, P2:
. (15)
(15)
Таким образом, масса покоя, вообще
говоря, не аддитивна. Например, пара фотонов, не
имеющих массу покоя, имеет массу покоя, если
фотоны летят в разные стороны, и не имеет массу
покоя, если фотоны летят в одну и ту же сторону.
Тем не менее, все три величины, P,
m, m0, подчиняются
закону сохранения, то есть не изменяются со
временем для замкнутой системы.
Однако ввиду неаддитивности массы
покоя, на наш взгляд, нецелесообразно
рассматривать массу покоя системы тел. Имеет
смысл говорить лишь о сумме масс покоя отдельных
тел системы. В действительности именно так
поступают на практике. Когда говорят, что при
неупругих соударениях увеличивается масса
покоя, имеют ввиду не массу покоя системы,
которая удивительным образом сохраняется
неизменной при соударениях благодаря
неаддитивности, а сравнивают именно сумму масс
покоя тел до столкновения и массу покоя после
столкновения. Точно так же, когда говорят о
Точно так же, когда говорят о
дефекте массы покоя при ядерных реакциях, имеют в
виду не массу покоя, определяемую формулой (15), а
сумму масс покоя частей системы.
6. Сравнение масс
Теперь уместно задать вопрос. Какую из
двух масс, массу покоя или инертную массу следует
назвать простым словом масса, обозначить буквой m без индексов и тем самым признать
«главной» массой. Это — не терминологическая
проблема. Здесь имеется серьезная
психологическая подоплека.
Чтобы решить, какая из масс — главная,
перечислим еще раз свойства обеих масс.
Масса покоя является постоянной
величиной для данного тела и выражает
«количество вещества тела». Она
соответствует привычному дорелятивисткому
ньютоновскому представлению о массе. Но она не
эквивалентна энергии, не эквивалентна
гравитационной массе, она не аддитивна и поэтому
не используется как характеристика системы
тел или частиц. Это последнее обстоятельство
вызывает путаницу (см. [1] , стр. 1365) и мешает
[1] , стр. 1365) и мешает
проявлению закона сохранения массы покоя. Фотоны
и частицы, движущиеся со скоростью света, не
обладают массой покоя. Операционное определение
массы покоя частицы предполагает торможение ее
до малой скорости без использования информации о
текущем состоянии частицы.
Инертная масса это — релятивистская
масса. Она принимает различное значение для
различных наблюдателей, аналогично тому, как
скорость хода часов оказывается различной
относительно различных наблюдателей. Инертная
масса эквивалентна энергии и гравитационной
массе, она аддитивна и подчиняется закону
сохранения. Инертной массой обладают частицы, не
имеющие массы покоя. Операционное определение
инертной массы основано на простой формуле P
= mv.
На наш взгляд, инертную массу следует называть
массой и обозначать m, как
это и делалось в настоящей статье.
7. Психологическая подоплека
К сожалению, большое количество
физиков считает массу покоя главной и обозначает
ее m а не m0, а инертную массу дискриминирует и
оставляет без обозначения, что вносит
дополнительную путаницу, поскольку из-за этого
порой бывает трудно понять, о какой массе идет
речь.
Эти физики соглашаются, например, с тем, что
масса газа увеличивается при нагревании, потому
что увеличивается содержащаяся в нем энергия, но
психологический барьер мешает им попросту
объяснить это увеличение ростом массы отдельных
молекул вследствие увеличения их тепловой
скорости.
Эти физики жертвуют представлением о массе как
мере инертности в пользу ярлыка, прикрепляемого
к каждой частице с информацией о неизменном
«количестве вещества», потому что ярлык
соответствует их привычному ньютоновскому
представлению о массе. Они считают, например, что
излучение, которое, согласно Эйнштейну [6] ,
«переносит инерцию между излучающими и
поглощающими телами», не имеет массы,
поскольку к излучению невозможно прикрепить
ярлык.
Инертная масса отсутствует в издаваемых сейчас
стандартных учебниках физики в России
(И.В.Савельев) и за рубежом [7,8], а также в
популярной литературе [9] . Этот факт, однако, скрыт
тем обстоятельством, что сторонники массы покоя
настойчиво называют массу покоя не массой покоя,
а просто массой, словом, которое ассоциируется с
мерой инерции.
Главная психологическая трудность заключается
в том, чтобы отождествить массу и энергию
(которая изменяется), чтобы принять эти две
сущности, как одну. Легко принять формулу E0
= m0c2 для
покоящегося тела. Труднее принять
справедливость формулы E = mc2 для любой скорости. Замечательная
формула E= mc2 представляется,
например, Л.Б. Окуню «безобразной» [10] .
Сторонники массы покоя, видимо, не в состоянии
принять идею инертной, релятивистской массы так
же, как ранее противники теории относительности
не могли принять относительность времени. Ведь
время жизни астронавта или нестабильной частицы
изменяется так же, как изменяется их инертная
масса: . Здесь уместно процитировать М.
Планка: «Великая научная идея редко внедряется
путем постепенного убеждения и обращения своих
противников, редко бывает, что Савл становится
Павлом. В действительности дело происходит так,
что оппоненты постепенно вымирают, а растущее
поколение с самого начала осваивается с новой
идеей. » [11] К сожалению, великая идея
» [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
«Известия вузов. Физика», «Квант», «American Journal of Physics»,
«Physics Education» (Bristol), «Physics Today».
8. Шварцшильдовское
пространство
Мы получим здесь формулу (10),
рассмотрев пространство-время Шварцшильда общей
теории относительности с выражением для
интервала s [12] :
.
Уравнения радиальной геодезической
линии могут быть получены по общей формуле,
использующей коэффициенты связности :
, (16)
. (17)
Первый интеграл уравнения (16) легко находится:
. (18)
Запишем теперь выражение для
ускорения a, учитывая (18) и
то, что соотношения между расстоянием l и временем , с одной стороны, и
координатами r, t, с
другой, даются формулами
, :
.
Выразив таким образом ускорение a через , мы можем теперь
воспользоваться уравнением (17), а затем,
вернувшись к l и ,
получить окончательно
, . (10)
Список литературы
1. Храпко Р. И. Что есть масса? // Успехи
физических наук. — 2000, N12. √ с.1363-1366.
2. Храпко Р. И. Что есть масса? — http://www.mai.ru. Труды
МАИ, Вып.2.
3. Фриш С. Э., Тиморева А. В. Курс общей
физики. Т. 3. — М.: ГИТТЛ, 1951.- 547 с.
4. Фейнман Р. и др. Фейнмановские лекции по
физике. Т. 1. — М.: Мир, 1965. √ 232 с.
5. Храпко Р. И., Спирин Г.Г., Разоренов В. М.
Механика. — М.: МАИ, 1993. √ 89 с.
6. Эйнштейн А. Зависит ли инерция тела от
содержащейся в нем энергии. // Принцип
относительности. — ОНТИ, 1935.- с.175-178.
7. Resnick R., Halliday D., Krane K. S. Physics. V.1 — N.Y.: J. Wiley, 1992.-592p.
8. Alonso M., Finn E. J. Physics — N.Y.: Addison-Wesley, 1995. -496p.
-496p.
9. Taylor E. F., Wheeler J. A. Spacetime Physics. √ San Francisco: Freeman, 1966.-
631c. Русский перевод: Тейлор Э. Ф.,
Уилер Дж. А. Физика пространства-времени. √ М.:
Мир, 1971.- 612c.
10. Окунь Л. Б. Понятие массы. // Успехи физических
наук. — 1989, т. 158. — с.512-530.
11. Планк М. Происхождение научных идей и влияние
их на развитие науки./ М. Планк.// Сборник статей к
столетию со дня рождения Макса Планка. — М.:
АНСССР, 1958.- с.52.
12. Ландау Л.Д., Лифшиц Е.М. Теория поля. — М.: Наука,
1973.- 504с.
Вес на различных планетах — урок. Физика, 9 класс.
Повседневно мы воспринимаем вес и массу тела как одно и то же. Обе эти величины очень связаны друг с другом, но это не одно и то же. Масса тела зависит от количества молекул и атомов в теле, её обозначают \(m\) и измеряют в килограммах. А вес — это сила, с которой тело действует на другие тела в результате гравитации, его обозначают \(P\) и измеряют в ньютонах, Н.
Пример:
в видеоролике «The difference between mass and weight»: http://www.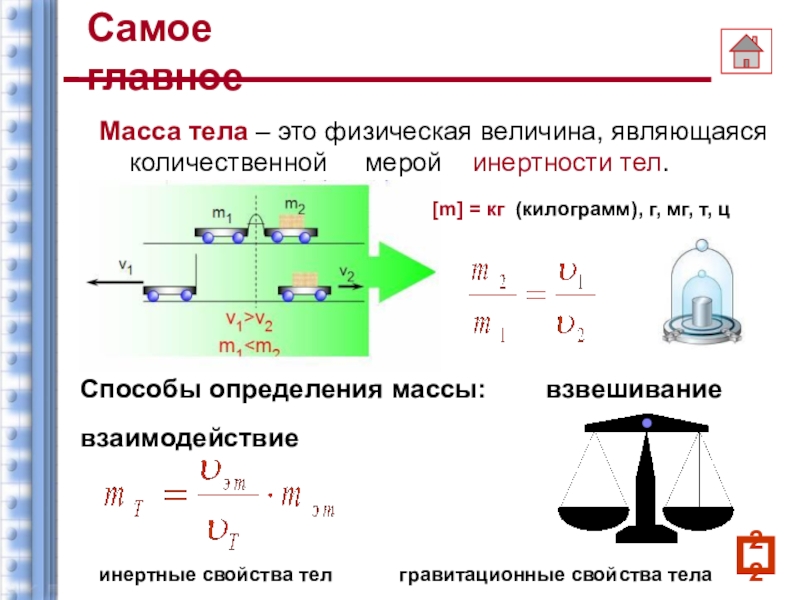 youtube.com/watch?v=_Z0X0yE8Ioc — рассматривается различие между весом и массой тела и поясняется, что вес тела мы ощущаем, когда пытаемся поднять тело вертикально вверх, а массу тела мы ощущаем как инерцию, когда пытаемся сдвинуть тело с места.
youtube.com/watch?v=_Z0X0yE8Ioc — рассматривается различие между весом и массой тела и поясняется, что вес тела мы ощущаем, когда пытаемся поднять тело вертикально вверх, а массу тела мы ощущаем как инерцию, когда пытаемся сдвинуть тело с места.
Вес тела — это сила, с которой тело давит на поверхность или растягивает подвес, на котором оно висит.
Обрати внимание!
Вес тела на Земле одинаков с силой тяжести, если тело находится в состоянии покоя или прямолинейного равномерного движения. Если тело ускоренно движется, тогда значения веса тела и силы тяжести могут отличаться.
Вес тела определяют по формуле P=m⋅g, где
\(P\) — вес тела, Н;
\(m\) — масса тела, кг;
\(g\) — ускорение свободного падения, мс2.
Устройство, которое используется для определения массы тела, называют весами, хотя на самом деле весы измеряют не массу, а вес тела. При градуировке шкалы весов учитывается, что, если вес тела на Земле равен \(9,8\) Н, то масса такого тела равна \(1\) кг. Если бы массу тела попытались определить при помощи весов на космической станции, которая находится в состоянии невесомости, тогда измерить вес тела не удалось бы, так как в этом случае вес тела был бы равен нулю, поскольку тело в состоянии невесомости не давит на поверхность весов. Следовательно, вес тела можно определить в гравитационном поле только тогда, когда тело не находится в состоянии невесомости (в состоянии свободного падения).
Если бы массу тела попытались определить при помощи весов на космической станции, которая находится в состоянии невесомости, тогда измерить вес тела не удалось бы, так как в этом случае вес тела был бы равен нулю, поскольку тело в состоянии невесомости не давит на поверхность весов. Следовательно, вес тела можно определить в гравитационном поле только тогда, когда тело не находится в состоянии невесомости (в состоянии свободного падения).
В Солнечной системе имеется восемь планет, и для каждой планеты характерна своя величина ускорения свободного падения. Это означает, что на каждой из планет одно и то же тело будет иметь различный вес.
Рис. \(1\). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун
Таблица \(1\). Величина ускорения свободного падения вблизи поверхности различных планет Солнечной системы
|
Небесное тело |
Ускорение свободного падения, мс2 |
|
Меркурий |
\(3,7\) |
|
Венера |
\(8,87\) |
|
Земля |
\(9,8\) |
|
Марс |
\(3,7\) |
|
Юпитер |
\(24,8\) |
|
Сатурн |
\(10,4\) |
|
Уран |
\(8,87\) |
|
Нептун |
\(10,15\) |
|
Плутон |
\(0,66\) |
|
Луна |
\(1,62\) |
|
Солнце |
\(274,0\) |
На Земле ускорение свободного падения в \(6\) раз больше, чем на Луне, поэтому вес космонавта на Луне будет в \(6\) раз меньше, чем на Земле.
Космонавт с массой \(120\) кг на Земле весит P=120⋅9,8=1176 Н, а на Луне его вес будет P=120⋅1,6=192Н.
Пример:
если нашими обычными весами измерить вес космонавта на Луне, тогда показание на шкале весов было бы не \(120\) кг, а всего лишь \(20\) кг.
Пример:
а вот на Солнце ускорение свободного падения почти в \(28\) раз больше, чем на Земле, поэтому на нём все тела казались бы тяжелее в \(28\) раз. Если бы мы могли космонавта с массой в \(120\) кг взвесить на поверхности Солнца, то весы показали бы, что космонавт весит \(3355\) кг. Конечно, в реальности это сделать мы не смогли бы, так как поверхность Солнца раскалена до температуры примерно 6000°С.
Узнать вес зная массу. Как найти массу, зная плотность и объем
Инструкция
Чтобы найти массу, зная плотность, разделите объем тела или вещества на его плотность. То есть воспользуйтесь формулой: m = V / ρ, где:V – объем,
ρ – плотность,
V – объем.Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения (СИ). Для этого, переведите объем (м³), а плотность – в на (кг/м³). В этом случае значение массы получится в килограммах.
Для этого, переведите объем (м³), а плотность – в на (кг/м³). В этом случае значение массы получится в килограммах.
Если плотность и объем заданы в одной системе единиц, то предварительный в СИ производить необязательно. Масса тела или вещества в таком случае будет измеряться в той единице , которая указана в числителе единицы измерения плотности (единицы измерения объема при расчете сократятся).
Так, например, если объем задан в литрах, а плотность в граммах на литр, то расчетная масса получится в граммах.
Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.
Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть:Vпр.пар. = a*b*c, где:Vпр.пар. – объем прямоугольного параллелепипеда, а
a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
В химии и физике часто попадаются задачи, в которых необходимо вычислить массу вещества, зная его объём. Как найти массу через объем. В этом вам поможет таблица плотностей, поскольку чтобы найти массу, необходимо знать и плотность, и объём вещества.
Если в условии задачи не указана плотность, можно посмотреть в таблицу, в которой есть такие данные о каждом веществе. В идеале, конечно, необходимо выучить такую таблицу, но можно обратиться и к учебнику по химии.
Правило гласит, что объём вещества, умножений на его плотность, равняется массе данного вещества. Из этого правила, выводится формула массы через объем. Она выглядит так: m = V*p. Где m — масса, V — объём, а p — плотность. Зная число, которое равно объёму, можно посмотреть число, которое будет равно плотности, умножить данные. Так можно получить массу.
Пример вычисления
Например, дан объём 5 мл. Объём вещества исчисляется в таких единицах, как литры и миллилитры. Вещество, массу которого нужно найти, — желатин. Посмотрев в таблице, можно увидеть, что его плотность равна 1,3 г./мл. Теперь воспользуйтесь формулой. Объём V равен 5 мл. Необходимо умножить 5 мл. на 1,3 г./мл. То есть: 5*1,3 = 6,5 грамм. Значит m — масса равна 6,5 грамм. Почему именно грамм: при умножении объёма на плотность, у нас есть такие единицы как миллиграммы. Их сокращаем, остаются граммы, которые и обозначают массу.
Можно воспользоваться и другим способом. Необходимо знать или иметь под рукой таблицу Менделеева. Этот метод подразумевает использование молярной массы вещества (в таблице). Необходимо знать формулу, которая гласит, что масса вещества равна произведению объёма на молярную массу. То есть m = V*M, где V — объём данного вещества, а М — его молярная масса.
Масса
Инертная масса
Гравитационная масса
Примеры решения задач
Решение.
Задание.
Какова масса 2м 3 меди?
Ответ.
(кг)
Краткая теория
Онлайн калькуляторы
Формула массы тела
Определение и формула массы тела
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.
Масса
– аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна сумме масс всех отдельных частей системы (m i):
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Формула расчета массы через плотность тела
Масса тела может быть рассчитана как:
где – плотность вещества тела, где интегрирование проводится по объему тела. Если тело однородное (), то масса может быть рассчитана как:
Масса в специальной теории относительности
В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:
где E – полная энергия свободного тела, p- импульс тела, c – скорость света.
Релятивистская масса частицы определяется формулой:
где m 0 – масс покоя частицы, v – скорость движения частицы.
Основной единицей измерения массы в системе СИ является: [m]=кг.
Примеры решения задач
Решение.
При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией. По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:
где E 1 – энергия первой частицы до удара, E 2 – энергия второй частицы до соударения.
Закон сохранения энергии запишем в виде:
Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:
Задание.
Какова масса 2м 3 меди?
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной Cu =8900 кг/м 3 . Для расчета все величины известны. Проведем вычисления:
Ответ.
(кг)
Краткая теория
Онлайн калькуляторы
Копирование материал с сайта возможно только с разрешения администрации портала и при наличие активной ссылки на источник.
http://www.webmath.ru/poleznoe/formules_21_2_massa_tela.php
Как найти массу?
Многие из нас в школьное время задавались вопросом: Как найти массу тела? Сейчас мы попытаемся ответить на этот вопрос.
Нахождение массы через его объем
Решить задачу, как найти массу вещества через его объем, довольно легко. Для этого следует применить формулу удельной плотности вещества
где p является удельной плотностью вещества;
v — занимаемым объемом.
В качестве меры массы будут использоваться граммы, килограммы и тонны. Меры объёмов: сантиметры кубические, дециметры и метры. Удельная плотность будет вычисляться в кг/дм, кг/м, г/см, т/м.
Таким образом, в соответствии с условиями задачи в нашем распоряжении есть бочка объемом двести литров. Это значит, что ее объем равняется 2 м.
Но вы хотите узнать, как найти массу. Из вышеназванной формулы она выводится так:
Сначала нам требуется найти значение р – удельной плотности дизельного топлива. Найти данное значение можно, используя справочник.
В книге мы находим, что р = 860,0 кг/м.
Затем полученные значения мы подставляем в формулу:
m = 860*2 = 1720,0 (кг)
Нахождение массы через плотность и объем
Очень часто в практических заданиях по физике можно встретить такие величины, как масса, плотность и объем. Для того чтобы решить задачу, как найти массу тела, вам требуется знать его объем и плотность.
Предметы, которые вам будут нужны:
2) Калькулятор (компьютер).
3) Емкость для измерения.
Теперь требуется решить задачу, как найти массу в соответствии с формулой d = m/V, где
m является массой предмета (в килограммах),
V является его объемом (в метрах кубических).
Таким образом, плотность вещества является массой единицы его объема.
Если вам необходимо найти плотность материала, из которого создан предмет, то следует воспользоваться таблицей плотностей, которую можно найти в стандартном учебнике по физике.
Объем предмета вычисляется по формуле V = h * S, где
H – высота предмета (м),
S – площадь основания предмета (м).
Зная объем V и плотность d предмета, вы можете легко найти его массу по формуле m = d * V. Перед тем, как вычислить массу, требуется привести все измерительные единицы в единую систему, например, в систему СИ, являющуюся интернациональной измерительной системой.
В соответствии с вышеназванными формулами можно сделать следующий вывод: для нахождения требуемой величины массы с известным объемом и известной плотностью требуется умножить значение плотности материала, из которого изготовлено тело, на объем тела.
http://fb.ru/article/50627/kak-nayti-massu
В фактических задачах по физике и математике зачастую встречаются такие величины как объем, масса и плотность
. Зная плотность и объем тела либо вещества, абсолютно допустимо обнаружить его массу
.
Вам понадобится
- – компьютер либо калькулятор;
- – рулетка;
- – мерная емкость;
- – линейка.
Инструкция
1.
Как вестимо, предметы, имеющие один и тот же объем, но сделанные из различных материалов, будут иметь различную массу (дерево и металл, стекло и пластмасса). Массы тел, изготовленных из одного и того же вещества (без пустот), прямо пропорциональны объему рассматриваемых предметов. Напротив говоря, непрерывной величиной является отношение массы предмета к его объему. Эта величина носит наименование «плотность вещества. В будущем обозначим ее буквой d.
2.
Исходя из определения, d=m/V, гдеm – масса предмета (кг),V — его объем (м3).Как видно из формулы, плотность вещества – это масса единицы его объема.
3.
Узнать плотность вещества, из которого изготовлен предмет, дозволено из таблицы плотностей в приложении к учебнику физики либо на сайте http://www.kristallikov.net/page15.html, где приведены плотности фактически всех существующих веществ.
5.
Если нет вероятности с точностью произвести измерение геометрических размеров тела, воспользуйтесь законом Архимеда. Для этого возьмите сосуд, имеющий шкалу (либо деления) для измерения объема жидкости, опустите предмет в воду (в сам сосуд, снабженный делениями). Объем, на тот, что увеличится содержимое сосуда, – и есть объем погруженного в него тела.
6.
Если вестимы плотность d и объем V предмета, неизменно дозволено обнаружить его массу, пользуясь формулой: m=V*d. Перед расчетом массы приведите все единицы измерения в одну систему, скажем, в международную систему измерения СИ.
7.
Итог из приведенных формул дальнейший: дабы получить желанное значение массы, зная плотность и объем, нужно умножить значение объема тела на значение плотности вещества, из которого оно сделано.
Массу
тела
традиционно определяют экспериментально. Для этого берут груз, ставят его на весы и получают итог измерения. Но при решении физических задач, приведенных в учебниках, измерение массы по объективным причинам нереально, но имеются те либо иные данные о теле. Зная эти данные, дозволено определить массу тела
неявно путем расчета.
Инструкция
1.
В школьных курсах физики, химии, астрономии дозволено встретить представление массы. По массе тела
находят обратные величины – объем, плотность, силу. Масса – количественный показатель вещества, следственно в задачах по химии число вещества находят, исходя из массы. Масса зависит от свойств вещества, из которого состоит тело, а также от числа этого вещества.Существует несколько основных способов расчета массы. Выбирают их в зависимости от того, какие другие физические величины заданы в задаче. Разглядим всякий случай по отдельности.
2.
Самый общеизвестный метод нахождения массы тела
– это ее расчет на основании объема и плотности. Правда, в ряде задач перед определением массы доводится рассчитывать сам объем, руководствуясь иными геометрическими колляциями тела
. Скажем, для цилиндра с знаменитыми площадью основания и высотой, изготовленного из вещества с вестимой плотностью, масса будет равна:m=?*V=?*S*h, где Vцил.=S*h, ? – плотность, S – площадь основания цилиндра, h – высота цилиндра.Если же объем указан в задаче прямо, для нахождения массы его довольно примитивно умножить на плотность:m=?*V
3.
Иной раздел физики, где доводится рассчитывать массу – динамика. Традиционно в нем изучается взаимодействие между тела
ми, действие внешних сил на тела
, состояние тел при равномерном движении. Всякое тело силой F получает убыстрение при взаимодействии с иным телом. При этом, оно некоторую массу m. Массы связана с силой дальнейшим соотношением:F=m*a, где a – убыстрение заданного тела
; m -масса тела
Отсюда дозволено узнать массу тела
:m=F/a
4.
В учебниках по химии мы встречаются представления числа вещества и молярной массы. Через эти две величины также дозволено выразить массу вещества.3Масса рассчитывается дальнейшим образом:m=p*V=7,8*314=24,492 г
Плотность
есть отношение массы к занимаемому ей объему – для твердых тел, и отношением молярной массы к молярному объему – для газов. В самом всеобщем виде объем (либо молярный объем) будет отношением массы (либо молярной массы) к ее плотности. Плотность
вестима. Что делать? Сперва определить массу, после этого вычислить объем, после этого внести нужные поправки.
Инструкция
1.
Объем газа равен отношению произведения числа вещества, умноженного на его молярную массу – к теснее вестимой плотности. Иными словами, даже зная плотность, нужно знать молярную массу газа и число вещества, то есть – сколько у вас есть моль газа. В тезисе, зная, сколько моль газа у вас есть, дозволено вычислить его объем, даже не зная плотности – согласно закону Авогадро, один моль всякого газа занимает объем 22,4 л. Если же непременно вычислять объем через плотность, то вам потребуется узнать массу газа в неведомом пока объеме.
2.
Объем твердого тела дозволено определить, даже не зная плотности, легко измерив его, а в случае трудной и дюже неправильной формы объем определяется, скажем, по объему вытесненной твердым телом жидкости. Впрочем, если нужно вычислять объем именно через плотность, то объем твердого тела есть отношение массы тела к его плотности, а масса обыкновенно определяется простым взвешиванием. Если же взвесить тело по каким-то причинам (скажем, оно слишком огромное либо движется) немыслимо, то придется прибегать к достаточно трудным косвенным расчетам. К примеру, для движущегося тела масса есть отношение удвоенной кинетической энергии к квадрату его скорости, либо отношение силы, приложенной к телу, к его убыстрению. Для дюже большого покоящегося тела придется прибегать к расчетам по отношению к массе Земли, с применением гравитационной непрерывной и момента вращения. Либо же – через вычисление удельной теплоемкости вещества; в любом случае умения только плотности для вычисления объема будет неудовлетворительно.
3.
Вычислив массу твердого тела, дозволено вычислить объем – простым делением массы на плотность.
Обратите внимание!
1. Указанные выше способы больше либо менее применимы только в случае однородности вещества, из которого состоит твердое тело2. Приведенные способы больше либо менее применимы в относительно тесном интервале температур – от минус 25 до плюс 25 градусов Цельсия. При изменении агрегатного состояния вещества плотность может меняться скачкообразно; в этом случае формулы и способы вычислений будут вовсе другими.
Масса как физическая величина – это параметр, характеризующий силу воздействия тела на гравитацию. Для расчета массы тела в физике
требуется знать две его величины: плотность материала тела и его объем.
Инструкция
1.
Пускай задано некое тело объемом V и плотностью его вещества p. Тогда его массу
подсчитывают так:m = p*V. Для наглядности приводится пример:Пускай дан алюминиевый брусок объемом 5 куб. метров. Плотность алюминия составляет 2700 кг./куб. метр. В таком случае масса бруска составит:m = 2700/5 = 540 кг.
Обратите внимание!
Представление массы зачастую путают с иной, не менее редко встречающейся, физической величиной – весом. Вес измеряется в н/м? и характеризует силу, которая воздействует на точку опоры. Масса же, по своей природе, не имеет какой бы то ни было точки опоры, и воздействует, как было подмечено, лишь на гравитацию Земли.
При решении некоторых физических задач требуется обнаружить плотность
тела
. Изредка плотность физического тела нужно определить и на практике, скажем, для того дабы узнать, утонет оно либо нет. Кстати, тело человека также дозволено отнести к физическим телам. Причем представление «плотности» человеческого тела давным-давно теснее вошло в обиход. Так «прочно сбитого» человека традиционно называют «плотным», а того, кто имеет противоположную конституцию тела – «рыхлым».
Вам понадобится
- калькулятор, весы, линейка, мерная кружка, таблица плотности веществ.
Инструкция
1.
Дабы обнаружить плотность физического тела, определите из какого вещества либо материала оно состоит. После этого возьмите таблицу плотности веществ и обнаружьте в ней соответствующее вещество. Так, скажем, если предмет изготовлен из алюминия, его плотность будет равна 2,7 г/см?.
2.
Если тело состоит из нескольких веществ, то обнаружьте в соответствующих таблицах плотность всего из них. Дабы обнаружить плотность тела в совокупности, определите взнос всего вещества в образование плотности предмета. Для этого определите объем либо массу всей однородной части, а после этого посчитайте массу и объем каждого тела.
3.
Пускай, скажем, тело состоит из 2-х частей массой m1 и m2, соответственно. Плотность всей части – ?1 и?2. Дабы обнаружить среднюю плотность тела, обнаружьте всеобщий объем: V = V1 + V2 = m1 * ?1 + m2 * ?2, а после этого поделите на всеобщую массу тела (m = m1 + m2): ? = V / m = (m1 * ?1 + m2 * ?2) / (m1 + m2), где:V – всеобщий объем тела;V1 и V2 – объем первой и 2-й части тела соответственно;m – всеобщая масса тела;m1 и m2 – масса первой и 2-й части тела соответственно;? – средняя плотность тела;?1 и?2 – плотность первой и 2-й части тела соответственно.
4.
Если знамениты объемы (V1 и V2) всей части тела, а также их плотности, для вычисления плотности тела воспользуйтесь аналогичной формулой:? = V / m = (V1 + V2) / (m1 + m2) = (V1 + V2) / (V1 / ?1 + V2 / ?2). Обозначения параметров те же, что и в предыдущей формуле.
5.
Если материал (вещество), из которого состоит тело, неведом либо имеет непостоянную плотность (скажем, дерево, плотность которого зависит от влажности), дабы обнаружить его плотность, определите его объем и поделите на массу. То есть воспользуйтесь формулой:? = V / m.Для этого, финально, придется посчитать либо измерить объем и массу тела, но такой способ даст самый точный итог. Если тело имеет форму примитивный геометрической фигуры, посчитайте его объем, воспользовавшись соответствующими формулами стереометрии. Объем трудных тел определите через объем вытесненной ими жидкости. Массу тела обнаружьте с поддержкой взвешивания.
Масса какого-нибудь тела является его важнейшей физической колляцией. В нынешней физической науке есть разграничение представления “масса”: гравитационная масса (как степень воздействия тела на земную гравитацию) и инертная масса (какое усилие понадобится для того, дабы вывести тело из состояния инерции). В любом случае обнаружить массу
дюже легко, если знамениты плотность
и объем тела.
Инструкция
1.
В том случае, если у тела знамениты такие показатели, как его объем (V) и плотность
(p), то для расчета массы тела понадобится применять формулу: m = p*V.
2.
Для наглядности дозволено привести пример. Требуется обнаружить массу
бетонной плиты, чей объем составляет 15 м?.Решение: для нахождения массы бетонной плиты требуется знать только лишь его плотность
. Для того, дабы узнать эту информацию, надобно воспользоваться таблицей плотностей разных веществ.
3.
Согласно этой таблице плотность
бетона составляет 2300 кг/м?. Тогда для того, дабы обнаружить массу
бетонной плиты, понадобится совершить примитивное алгебраическое действие: m = 15*2300 = 34500 кг, либо 34.5 тонн. Результат: масса бетонной плиты составляет 34.5 тонн
4.
Измерение массы традиционным методом происходит при помощи одного из древнейших приборов общества – с поддержкой весов. Это происходит вследствие сопоставлению массы тела с подмогой эталонной массы груза – гирь.
Обратите внимание!
Проводя расчет по указанной выше формуле, нужно осмысливать, что таким образом узнается масса покоя данного тела. Увлекателен факт того, что многие элементарные частицы владеют колеблющейся массой, которая зависит от скорости их движения. Если элементарная частица движется со скоростью тела, то эта частица является безмассовой (скажем, фотон). Если же скорость движения частицы ниже скорости света, то такая частица именуется громоздкой.
Полезный совет
При измерении массы никогда невозможно забывать, в какой системе будет дан финальный итог. Имеется ввиду, что в системе СИ масса измеряется в килограммах, в то время как в системе СГС масса измеряется в граммах. Также масса измеряется в тоннах, центнерах, каратах, фунтах, унциях, пудах, а также во многих других единицах в зависимости от страны и культуры. В нашей стране, к примеру, массу издавна измеряли в пудах, берковцах, золотниках.
У вас есть двухсотлитровая бочка. Вы планируете ее всецело заправить дизельным топливом, которое используете для отопления своей мини-котельной. А сколько она будет весить, наполненная соляром? Теперь вычислим.
Вам понадобится
- – таблица удельной плотности веществ;
- – знание изготавливать простейшие математические вычисления.
Инструкция
1.
Дабы обнаружить массу вещества по его объему, воспользуйтесь формулой удельной плотности вещества.p = m/vздесь p – удельная плотность вещества;m – его масса;v – занимаемый объем. Массу будем считать в граммах, килограммах и тоннах. Объемы в кубических сантиметрах, дециметрах и мерах. И удельную плотность, соответственно, в г/см3, кг/дм3, кг/м3, т/м3.
2.
Выходит, по условиям задачи, у вас есть двухсотлитровая бочка. Это значит: бочка емкостью 2 м3. Двухсотлитровой ее называют, так как воды, с ее удельной плотностью равной единице, в такую бочку входит 200 литров.Вас волнует масса. Следственно выводите ее в представленной формуле на первое место.m = p*vВ правой части формулы незнакомо значение р – удельная плотность дизельного топлива. Обнаружьте его по справочнику. Еще проще – задать в поиск запрос в интернете «удельная плотность дизельного топлива».
3.
Обнаружили: плотность летнего дизельного топлива при t = +200 С – 860 кг/м3.Подставляйте значения в формулу:m = 860*2 = 1720 (кг)1 тонна и 720 кг – столько весят 200 литров летнего дизельного топлива. Завесив заблаговременно бочку, дозволено рассчитать всеобщий вес и прикинуть мощность стеллажа под бочку с соляром.
4.
В сельской местности пригодным бывает заблаговременно рассчитать массу нужных по кубатуре дров, дабы определиться с грузоподъемностью транспорта, на котором будут доставляться эти дрова. К примеру, вам на зиму нужен минимум в 15 куб. метров березовых дров. Ищите в справочной литературе плотность березовых дров. Это: 650 кг/м3.Вычисляйте массу, подставив значения в ту же формулу удельной плотности.m = 650*15 = 9750 (кг)Сейчас, исходя из грузоподъемности и вместимости кузова, вы можете определиться с видом транспортного средства и числом поездок.
Видео по теме
Обратите внимание!
Люди постарше огромнее знакомы с представлением удельного веса. Удельная плотность вещества – это то же, что и удельный вес.
Бывают обстановки, когда нужно вычислить массу
жидкости
, содержащейся в какой-нибудь емкости. Это может быть и во время учебного занятия в лаборатории, и в ходе решения бытовой загвоздки, скажем, при ремонте либо покраске.
Инструкция
1.
Самый легкой способ – прибегнуть к взвешиванию. Вначале взвесьте емкость совместно с жидкостью, потом перелейте жидкость в иную емкость, подходящую по размерам, и взвесьте пустую тару. А после этого остается лишь вычесть из большего значения меньшее, и вы получите результат. Разумеется, к этому методу дозволено прибегать, только имея дело с невязкими жидкостями, которые позже перелива фактически не остаются на стенках и днище первой емкости. То есть, какое-то число и тогда останется, но оно будет настоль немного, что им дозволено пренебречь, на точности вычислений это примерно не отразится.
2.
А если жидкость вязкая, скажем, глицерин? Как тогда определить ее массу
? В этом случае вам нужно знать ее плотность (?) и занимаемый объем (V). А дальше теснее все элементарно. Масса (М) вычисляется по формуле М = ?V. Разумеется, перед вычислением нужно перевести сомножители в цельную систему единиц.
3.
Плотность жидкости
дозволено обнаружить в физическом либо химическом справочнике. Но класснее воспользоваться измерительным прибором – плотномером (денситометром). А объем дозволено вычислить, зная форму и габаритные размеры емкости (если она имеет верную геометрическую форму).2h/4.
4.
Представим, вам задана такая задача. В ходе лабораторного эксперимента, жидкость массой m, находящаяся в емкости калориметра и имеющая теплоемкость с, была нагрета от изначальной температуры t1 до финальной температуры t2. На данный нагрев было затрачено число теплоты, равное Q. Какова масса этой жидкости
?
5.
Все величины, помимо m, знамениты, потерями тепла в ходе эксперимента дозволено пренебречь. В вычислении нет безусловно ничего трудного. Нужно лишь припомнить формулу, объединяющую число теплоты, массу
жидкости
, ее теплоемкость и разницу в температурах. Она такова: Q = mc(t2-t1). Следственно, масса жидкости
вычисляется по формуле: m = Q/c(t2-t1). Подставив в формулу вестимые вам величины, вы легко вычислите массу
жидкости
m.
Значение непрерывной Планка, обозначаемой буквой h, определено экспериментально в лабораторных условиях с точностью до десяти знаков позже запятой. Поставить навык по ее определению дозволено и в физическом кабинете, но точность будет гораздо поменьше.
Вам понадобится
- – фотоэлемент с внешним фотоэффектом;
- – источник света с монохроматором;
- – плавно регулируемый источник питания на 12 В;
- – вольтметр;
- – микроамперметр;
- – лампа на 12 В, 0,1 А;
- – калькулятор, работающий с числами, представленными в экспоненциальной форме.
Инструкция
1.
Используйте для навыка фотоэлемент с внешним фотоэффектом. Элемент с внутренним фотоэффектом (т.е., не вакуумный, а полупроводниковый) не подойдет. Испытайте его на пригодность для проведения навыка, для чего подключите к микроамперметру непринужденно, соблюдая полярность. Направьте на него свет – стрелка должна отклониться. Если этого не произойдет, используйте фотоэлемент иного типа.
2.
Не меняя полярности подключения ни фотоэлемента, ни микроамперметра, разорвите цепь и включите в ее обрыв регулируемый источник питания, выходное напряжение которого дозволено плавно менять от 0 до 12 В (с двумя ручками для дерзкой и точной регулировки). Внимание: включать данный источник следует не в прямой, а в обратной полярности, дабы он своим напряжением не увеличивал, а сокращал ток через элемент. Параллельно ему подключите вольтметр – на данный раз в полярности, соответствующей обозначениям на источнике. Этого дозволено не делать, если в блоке имеется встроенный вольтметр. Также подключите параллельно выходу нагрузку, скажем, в виде лампы на 12 В, 0,1 А, на случай, если внутреннее сопротивление источника крупно. Свет лампы попадать на фотоэлемент не должен.
3.
Установите напряжение источника на нуль. Направьте в фотоэлемент поток света из источника с монохроматором, выставив длину волны порядка 650 нанометров. Плавно увеличивая напряжение источника питания, добейтесь, дабы ток через микроамперметр стал равным нулю. Оставьте регулятор в этом расположении. Запишите показания вольтметра и шкалы монохроматора.
4.
Выставьте на монохроматоре длину волны порядка 450 нанометров. Немножко увеличьте выходное напряжение источника питания, дабы ток через фотоэлемент вновь стал равным нулю.(-34) Дж·с, навык дозволено считать поставленным положительно.
Видео по теме
Обратите внимание!
Соблюдайте осторожность при работе с электрическим оборудованием.
Универсальное уравнение для оценки идеальной массы тела и массы тела при любом ИМТ
Am J Clin Nutr. 2016 May; 103 (5): 1197–1203.
Кортни М. Петерсон
2 Лаборатория физиологии скелетных мышц Джона С. Макилхенни и
Диана М. Томас
4 Центр количественных исследований ожирения, Государственный университет Монклера, Монклер, Нью-Джерси;
Джордж Л. Блэкберн
5 Центр изучения медицины питания, Медицинский центр Бет Исраэль Дьяконис, Бостон, Массачусетс; и
6 Отдел питания Гарвардской медицинской школы, Бостон, Массачусетс
Стивен Б. Хеймсфилд
3 Лаборатория метаболизма и состава тела, Центр биомедицинских исследований Пеннингтона, Система государственного университета Луизианы, Батон-Руж, Луизиана;
2 Лаборатория физиологии скелетных мышц Джона С. Макилхенни и
3 Лаборатория метаболизма и состава тела, Центр биомедицинских исследований Пеннингтона, Университет штата Луизиана, Батон-Руж, Луизиана;
4 Центр количественных исследований ожирения, Государственный университет Монклера, Монклер, Нью-Джерси;
5 Центр изучения медицины питания, Медицинский центр диаконис Бет Исраэль, Бостон, Массачусетс; и
6 Отдел питания Гарвардской медицинской школы, Бостон, Массачусетс и Центр трансляционных наук.
Поступила 7 августа 2015 г .; Принято 25 февраля 2016 г.
Авторские права © Американское общество питания, 2016 г.
См. Статью на странице 1193.
Эта статья цитируется в других статьях PMC.
Abstract
Предпосылки: Уравнения идеальной массы тела (IBW) и диапазоны индекса массы тела (BMI) использовались для определения диапазонов здорового или нормального веса, хотя эти два разных подхода расходятся друг с другом. В частности, прошлые уравнения IBW несовместимы со значениями ИМТ, и, в отличие от ИМТ, в уравнениях не учитывается наличие диапазона идеальной или целевой массы тела.
Цель: Впервые, насколько нам известно, мы объединили концепции линейного уравнения IBW и определения целевого веса тела с точки зрения ИМТ.
Дизайн: С использованием расчетов и приближений мы получили простое в использовании линейное уравнение, которое врачи могут использовать для расчета как IBW, так и массы тела при любом целевом значении BMI. Мы измерили эмпирическую точность уравнения с использованием данных NHANES и провели сравнительный анализ с предыдущими уравнениями IBW.
Результаты: Наше линейное уравнение позволило нам рассчитать массу тела для любого ИМТ и роста со средней эмпирической точностью 0,5–0,7% на основе данных NHANES. Более того, мы показали, что наше уравнение массы тела напрямую согласуется со значениями ИМТ как для мужчин, так и для женщин, что позволяет избежать проблем с переоценкой и недооценкой на верхнем и нижнем концах спектра роста, которые преследовали предыдущие уравнения IBW.
Выводы: Наше линейное уравнение увеличивает сложность уравнений IBW, заменяя их одним универсальным уравнением, которое рассчитывает как IBW, так и массу тела при любом целевом ИМТ и росте.Таким образом, наше уравнение совместимо с ИМТ и может применяться с использованием математических вычислений или калькулятора без необходимости в приложении, что делает его полезным инструментом как для практикующих врачей, так и для широкой публики.
Ключевые слова: ИМТ, идеальная масса тела, ожирение, избыточный вес, упрощенные уравнения
См. Соответствующую редакционную статью на странице 1193.
ВВЕДЕНИЕ
Как точно определить желаемый или целевой вес тела для оценки питания и здоровья был важным вызов уже более века (1, 2).Многие из первых попыток были основаны на актуарных данных и определяли идеальный или желаемый вес тела с использованием таблиц роста и веса. Поскольку эти таблицы громоздки в использовании, уравнения идеальной массы тела (IBW) для прогнозирования веса как линейной функции от роста были разработаны, начиная с конца 1800-х годов (2). Позже популярность уравнений IBW возросла после того, как Хамви (3) и Девайн (4) опубликовали свои основополагающие уравнения (4). Десять лет спустя, мотивированные приложениями к дозированию лекарств, Robinson et al.(5) и Miller et al. (6) сформулировали уравнения IBW на основе таблиц роста и веса Metropolitan Life Insurance Company 1959 и 1983 годов соответственно. Совсем недавно Хаммонд (7) создал метрическую версию уравнения Хамви. Хотя уравнения IBW не так популярны, как когда-то, они все еще используются клиницистами для расчета дозировки лекарств, оценки статуса избыточного и недостаточного веса, а также для расчета потребления питательных веществ (2).
Преимущество уравнений IBW заключается в том, что они предсказывают вес (переменная: Wt) как линейная функция от высоты (переменная: Ht) как
, где a — наклон, а b — точка пересечения.Часто термин «рост» выражается как разница от эталонного значения, такого как рост в дюймах, превышающий 5 футов. Например, уравнения Хамви (3) для конкретных полов, разработанные для системы США, оценивают IBW для для мужчин —
, а для женщин —
, тогда как уравнения Девайна (4) для конкретных полов, которые были разработаны для метрической системы, оценивают IBW для мужчин как
, а для женщин как
, где Ht выражается в дюймах, а Ht составляет ≥60 дюймов. Простая линейная структура этих уравнений позволяет легко вычислить их с помощью мысленной математики или калькулятора.
Однако, несмотря на преимущество простоты, подход IBW имеет 3 важных ограничения. Во-первых, хотя IBW или желаемый вес изначально определялся как вес, связанный с максимальной продолжительностью жизни на каждом росте, не существует единого идеального веса, который универсально применим ко всем сопутствующим заболеваниям и причинам, связанным со смертностью, и не существует единого идеального веса, который можно было бы использовать. применимо ко всем демографическим факторам, включая возраст и этническую принадлежность (8). Во-вторых, уравнения IBW предсказывают единственную целевую массу тела, тогда как большинство клиницистов предпочитают диапазон целевых масс тела, а эмпирические данные подтверждают это.В-третьих, Shah et al. (2) проанализировали уравнения IBW и показали, что они несовместимы с BMI и, вместо этого, что уравнения IBW занижали массу тела при меньшем росте и завышали массу тела при более высоком росте (2). По этим причинам уравнения IBW в значительной степени были заменены диапазонами BMI.
Напротив, ИМТ, который определяется как масса тела, разделенная на квадрат роста (кг / м 2 ), в настоящее время более широко используется в клинических условиях для диагностики избыточного ожирения и недостаточного веса (9–11).ИМТ имеет два важных преимущества: он позволяет количественно оценить ожирение независимо от роста, и врачи могут использовать ИМТ для определения целевого диапазона веса. Диапазон ИМТ 18,5–24,9 часто рассматривается как диапазон идеального или здорового веса тела [хотя более свежие данные, например, предоставленные Flegal et al. (12) предположили, что несколько более высокие ИМТ связаны с более низкой смертностью], тогда как ИМТ варьируется для статуса избыточного веса (25,0–29,9), ожирения 1 класса (30–34,9; низкий риск), ожирения 2 класса (35.0–39,9; умеренный риск) и ожирение 3 класса (≥40,0; высокий риск) используются для определения риска сопутствующих заболеваний, связанных с ожирением. Таким образом, хотя ИМТ сложнее рассчитать, и врачи часто используют приложения для его расчета, этот недостаток обычно перевешивается тем фактом, что можно назначить диапазон целевых весов и что диапазоны более точно связаны с результатами для здоровья.
Эти проблемы приводят к важному вопросу о том, действительно ли уравнения IBW и ИМТ несовместимы или есть способ объединить 2 разных подхода к определению целевого веса тела.Насколько нам известно, впервые мы объединяем концепции уравнения IBW и ИМТ для определения целевого веса тела. Мы показываем, что одно линейное уравнение может оценить как IBW, так и целевую массу тела для любого BMI и роста. В процессе мы показываем, что преимущества уравнений IBW и BMI могут быть объединены в одно простое в использовании уравнение.
МЕТОДЫ
Математический вывод
Хотя концепция ИМТ предсказывает, что вес тела взрослого человека изменяется как криволинейная функция роста (т.е., Wt ∝ Ht 2 ), это соотношение можно оценить с помощью линейного уравнения в пределах 95% диапазона роста населения США (∼60–75 дюймов или ∼1,5–1,9 м) (13). Однако, в отличие от предыдущих подходов к разработке уравнений IBW, мы строго доказали, что линейная функция верна с использованием исчисления. В процессе мы использовали ключевые этапы вывода, чтобы создать новое уравнение веса тела, которое является более точным, чем предыдущие уравнения IBW, и может быть обобщено на любой ИМТ и рост.
Сначала мы преобразовали уравнение для веса тела как функции роста в форму
Затем мы преобразовали уравнение 6 и расширили его до контрольной высоты Ht 0 следующим образом:
, где
и Ht — это рост человека ().Используя вычислительную технику разложения Тейлора и сохраняя только члены, линейные по ΔHt, мы получили линейное приближение
Это приближение оправдано, только если процентная погрешность мала. Поскольку кривая почти линейна в диапазоне высот 95%, процентная погрешность действительно мала (). Здесь процентная погрешность определялась пренебрегаемым членом в разложении в ряд Тейлора
Эту погрешность можно вычислить напрямую. Например, если эталонная высота находится в середине диапазона высот 95%, максимальная процентная ошибка равна 1.0%.
Wt почти линейно зависит от Ht. Хотя Wt масштабируется как Ht 2 , Wt является почти линейной функцией Ht в диапазоне 95% Ht (∼1,5–1,9 м). Пример для ИМТ 27 кг / м 2 и показывает эталонный Ht ( Ht 0 ) 1,5 м и Δ Ht , который представляет собой разницу между Ht человека и эталонным Ht 0 . Ht, высота; Вес, вес.
Для согласования с предыдущими уравнениями IBW мы выбрали базовую высоту Ht 0 равной 5 футам (60.0 дюймов или 1,52 м) в системе США и 1,5 м (59,1 дюйма) в метрической системе. Однако этот выбор Ht 0 на нижнем конце 95% диапазона высоты вызывал ошибку. Поэтому мы аппроксимировали квадратичный член, показанный в уравнении 10 , компенсирующим линейным членом, который соответствовал массе тела на верхнем конце 95% диапазона роста (75 дюймов или 1,9 м). После стратегического округления наше окончательное уравнение было близко к точным касательным и секущим линиям, но дает более точную оценку веса тела, чем любая из этих линий.
В нашем выводе было два ключевых шага, которые сделали наш подход превосходящим предыдущие уравнения IBW. Во-первых, найдя выражение для переменной наклона a в уравнении 1 в терминах ИМТ, наше уравнение напрямую согласуется со значениями ИМТ. Такое согласование дает то преимущество, что наше уравнение можно использовать для расчета массы тела при любом целевом значении ИМТ, что, насколько нам известно, никогда раньше не делалось для уравнения IBW. Во-вторых, если выбрать подходящий компенсирующий линейный член (как описано ранее), наше уравнение IBW станет более точным и легко запоминающимся.
Сравнительный анализ
Мы рассчитали точность выведенного нами уравнения IBW как теоретическими, так и эмпирическими методами. Теоретическая точность рассчитывалась как абсолютная ошибка и процентная погрешность между точным и прогнозируемым весом тела в 95% -ном диапазоне роста (60–75 дюймов или 1,5–1,9 м) при значениях ИМТ 20 и 35. Эмпирическая точность (оба значения: абсолютная ошибка и ошибка в процентах) была рассчитана путем применения нашего уравнения к антропометрическим данным, собранным у взрослых в рамках NHANES 1999–2006 гг.Мы также сравнили, насколько хорошо наше уравнение веса тела и другие уравнения IBW соответствуют значениям ИМТ. Согласование со значениями ИМТ — это один из методов оценки степени соответствия уравнений IBW. Чтобы определить выравнивание, мы использовали программу Mathematica (версия 10.0; Wolfram Research) для вычисления конечного интеграла процентной ошибки каждого уравнения IBW с использованием веса тела, предсказанного ИМТ, в качестве истинного веса. Конечные интегралы были оценены в диапазоне высоты 95% и разделены на разницу между верхней и нижней границами диапазона высоты 95%, чтобы получить среднюю точность.Этот процесс повторяли для каждого значения ИМТ от 17,0 до 27,0 с шагом 0,1, и наименьшее значение средней процентной ошибки в этом диапазоне ИМТ принималось за истинную процентную ошибку для каждого уравнения IBW. Этот метод нахождения наименьшей процентной ошибки правильно учитывает тот факт, что некоторые уравнения IBW согласуются с более высокими ИМТ, тогда как другие уравнения лучше согласуются с более низкими ИМТ и, таким образом, позволяют избежать несправедливого наказания определенных уравнений на этом основании.
РЕЗУЛЬТАТЫ
Уравнение в системе США
Мы начали с вывода уравнения для системы США.Выведя уравнение, как описано в разделе «Методы», мы преобразовали вес в фунты, а рост в дюймы и расширили его вокруг эталонной высоты 5 футов (60 дюймов), чтобы получить
. Затем мы округлили 5,121 до 5 и пренебрегли показанным членом второго порядка. в уравнении 10 . Поскольку пренебрежение этим термином несколько занижало вес тела на верхнем конце 95% диапазона роста (ошибка 2,4%), мы нашли линейное приближение для замены члена второго порядка. После выполнения процедуры, изложенной в разделе «Методы», мы обнаружили, что поправочный член для уравнения 10 , необходимый для получения правильного веса на верхнем конце 95% диапазона роста, был
. После того, как этот результат был подставлен обратно в уравнение, мы получили
Клинические применения
Эта легко запоминающаяся формула обеспечивает высокоточный прогноз веса тела при любом целевом ИМТ и росте.Чтобы определить массу тела в фунтах, желаемый ИМТ умножается на 5, а затем прибавляется ИМТ / 5 фунтов на каждый дюйм роста> 5 футов. Например, для ИМТ 20 начните со 100 фунтов на рост 5 футов и добавьте 4 фунта на каждый дополнительный дюйм роста. Для ИМТ 25 начните со 125 фунтов и добавьте 5 фунтов на каждый дюйм роста. Таким образом, выразив наклон через ИМТ, мы разработали уравнение, которое действительно для прогнозирования массы тела при любом заданном ИМТ, что делает его единым универсальным уравнением.
В конкретном случае оценки IBW выбирается идеальный BMI для использования в уравнении; этот выбор объединяет концепции уравнений BMI и IBW.Например, если предположить, что ИМТ, равный 20, соответствует ИМТ, наше уравнение предсказывает, что ИМТ будет
. В качестве альтернативы, значения ИМТ в диапазоне от 18,5 до 25,0 могут быть взяты для представления диапазона ИМТ. В этом случае наше уравнение даст нижнюю границу (18,5) для IBW как
и верхнюю границу (25) как
. Аналогичным образом, другие диапазоны BMI также могут быть определены с помощью нашего уравнения. показаны расчеты с использованием нашего уравнения при ключевых значениях ИМТ 20, 25, 30, 35, 40, 45 и 50.Каждое увеличение ИМТ на 5 добавляет 25 фунтов к массе тела при росте 5 футов и дополнительно на 1 фунт за каждое увеличение роста на 1 дюйм; этот расчет обеспечивает удобный способ запомнить уравнение, поскольку большинство ключевых значений ИМТ кратны 5.
ТАБЛИЦА 1
Уравнение массы тела при ключевых значениях ИМТ
| ИМТ, кг / м 2 | Версия для США | Метрическая версия |
| Вес (фунт) = 5 × ИМТ + (ИМТ ÷ 5) × (Высота — 60 дюймов) | Вес (кг) = 2.2 × ИМТ + 3,5 × ИМТ × (Ht — 1,5 м) | |
| 20 | Wt (фунт) = 100 + 4 × (Ht — 60 дюймов) | Wt (кг) = 44 + 70 × (Ht — 1,5 м) |
| 25 | Wt (фунт) = 125 + 5 × (Ht — 60 дюймов) | Wt (кг) = 55 + 88 × (Ht — 1,5 м) |
| 30 | Wt (фунты) = 150 + 6 × (Ht — 60 дюймов) | Wt (кг) = 66 + 105 × (Ht — 1,5 м) |
| 35 | Wt (фунты) = 175 + 7 × (Ht — 60 дюймов) | Wt (кг) = 77 + 123 × (Ht — 1.5 м) |
| 40 | Wt (фунт) = 200 + 8 × (Ht — 60 дюймов) | Wt (кг) = 88 + 140 × (Ht — 1,5 м) |
| 45 | Wt (фунты) = 225 + 9 × (Ht — 60 дюймов) | Wt (кг) = 99 + 158 × (Ht — 1,5 м) |
| 50 | Wt (фунты) = 250 + 10 × (Ht — 60 дюймов) | Wt (кг) = 110 + 175 × (Ht — 1,5 м) |
Еще одна полезная особенность уравнения состоит в том, что каждое увеличение ИМТ человека на 1 пункт добавляет
массы тела.Например, каждое увеличение ИМТ на 1 пункт добавляет 6 фунтов массы тела человеку с ростом 5 футов 5 дюймов, 7 фунтов тому, чей рост составляет 5 футов 10 дюймов, и 8 фунтов тому, чей рост составляет 6 футов 3 дюйма. in. Знание о том, что потеря того же постоянного количества фунтов приблизительно снижает ИМТ человека на 1 пункт, может быть полезной и мотивирующей целью для людей, которые пытаются похудеть. И наоборот, при инверсии этого отношения ИМТ человека можно оценить, разделив массу его тела (в фунтах) на 6 фунтов, если рост человека составляет 5 футов 5 дюймов, на 7 фунтов, если рост человека составляет 5 футов 10 дюймов, и на 8 фунтов, если рост человека 6 футов 3 дюйма.Этот метод позволяет человеку быстро оценить ИМТ.
Практический пример, показывающий, как можно использовать это уравнение, можно увидеть в его применении к пациенту с массой тела 225 фунтов и ростом 5 футов 10 дюймов (или 70 дюймов). Если клиницист хочет знать, страдает ли пациент ожирением и какой вес ему необходимо сбросить, чтобы достичь верхнего предела диапазона IBW, быстрый расчет показывает, что вес пациента при ИМТ ожирения 30 составляет
, тогда как при верхний предел диапазона здорового ИМТ (<25), пациент будет иметь вес
Таким образом, мы классифицируем пациента как страдающего ожирением, и ему или ему нужно будет сбросить 50 фунтов, чтобы считаться нормальным или здоровым диапазон веса.Конечно, для многих пациентов цель по снижению веса на 5–10% может быть более реалистичной, и наше уравнение может учитывать такие персонализированные цели, поскольку оно позволяет оценить массу тела для любого желаемого целевого ИМТ. Например, если ИМТ 28,0 является желаемой целью пациента, целевой вес пациента будет
Уравнение в метрической системе
Для метрической системы мы использовали ту же математическую процедуру, что и для системы США. Уравнение:
, где мы округлили все члены до одного десятичного знака.Для справки: если мы возьмем версию уравнения для США и напрямую переведем ее в метрические единицы, то получим 3,6 вместо 3,5. Однако значение 3,5 дает более низкую совокупную процентную ошибку в диапазоне 95% высоты и, таким образом, является предпочтительным.
Точность
Наше уравнение очень точное. В, мы иллюстрируем теоретическую точность нашего уравнения для ИМТ 20 и 35. За исключением высоты ≤61 дюйм (≤1,53 м), уравнение предсказывает правильный вес с точностью до 1 фунта (0.5 кг) для ИМТ 20 и с точностью до 2 фунтов (1 кг) для ИМТ 35. Точность нашего уравнения, измеренная с помощью процентной ошибки, не зависит от ИМТ; таким образом, более высокие ИМТ не приводят к большему проценту ошибок. Максимальная процентная погрешность в 95% диапазоне высоты составляет 2,4% для обеих версий уравнения, а уравнение наиболее точное в середине диапазона высот, что является следствием того факта, что оно было разработано таким образом, чтобы минимизировать процентную ошибку. . Наконец, применительно к данным NHANES, наше уравнение дало среднюю эмпирическую точность 0.7% (95% ДИ: 0%, 3,2%) и 0,5% (95% ДИ: 0,3%, 2,4%) для версии США и метрической системы соответственно; это соответствовало средней абсолютной погрешности 1,1 фунта и 0,4 кг соответственно. Ошибка была вызвана в основном людьми с коротким и высоким концом диапазона роста, а влияние ковариат, таких как возраст, было опосредовано лишь косвенно, через их влияние на рост.
ТАБЛИЦА 2
Точность уравнения массы тела 1



